MatheAss 10.0 − Geometria 3D
Sistemi di coordinati
Trasformazione fra le coordinate cartesiane, le coordinate polari e le coordinate cilindriche.
cartesiano polare cilindrica x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Solidi di Platon
Tutti gli elementi di un tetraedro, un esaedro, un ottaedro, un dodecaedro e un icosaedro sono calcolato.
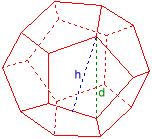
Esempio dodecaedro :
Dato:
¯¯¯¯
Diag. della faccia d = 2
Results:
¯¯¯¯¯¯¯
Bordo a = 1,236068
Altezza superficiale h = 1,902113
Sfera circoscr. rc = 1,7320508
Sfera inscritta ri = 1,3763819
Volume V = 14,472136
Area S = 31,543867
Altri solidi
Tutti gli elementi di un prisma regolare, di un cilindro circolare destro, di una piramide quadrata, di un cono circolare destro o di una sfera sono calcolato.
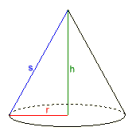
Esempio: Cono circolare
Given:
¯¯¯¯¯¯
Volume V = 1
Base B = 1
Results:
¯¯¯¯¯¯¯
Radius r = 0,56418958
Altitude h = 3
Apothem s = 3,0525907
Lateral Surface L = 5,4105761
Surface S = 6,4105761
Retta tra due punti
Retta tra A(1|1|1), B(2|5|6)
L'equazione vettoriale
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Distanza dall'origine
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Proiezione sul piano xy
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Proiezione :-4·x + y = 3
Punto inters. : S1(0,8|0,2|0)
Angolo inters.: 50.490288°
Proiezione sul piano yz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Proiezione :-5·x + 4·y = 1
Punto inters. : S2(0|-3|-4)
Angolo inters.: 8.8763951°
Proiezione sul piano xz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Proiezione -5·x + y = 4
Punto inters. S3(0,75|0|-0,25)
Angolo inters. 38.112927°
Piano tra tre punti
Piano attraverso i punti:
A(1|2|3), B(2|3|3), C(1|0|1)
L'equazione vettoriale:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
L'equ. in coordinate:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Distanza dall'origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Punti di traccia:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Sx (2|0|0)
Sy (0|-2|0)
Sz (0|0|2)
Sfera tra 4 punti
Sfera attraverso i punti:
A(1|0|0), B(0|2|0),
C(0|0|3), D(1|0|1)
Forma normale:
¯¯¯¯¯¯¯¯¯¯¯¯
⎧ -> ⎧-2,5 ⎫ ⎫2
K : ⎪ x - ⎪-0,5 ⎪ ⎪ = 12,75
⎩ ⎩ 0,5 ⎭ ⎭
Il centro e il raggio:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-2,5|-0,5|0,5)
r = 3,5707142
Intersezioni nello spazio
Il programma calcola le intersezioni di rette, piani e sfere.
Due rette
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Punto di intersezione:
S (5|5|5)
Angolo tra g e h: 60°
Distanze originali:
d(O,g) = 5 d(O,h) = 5
Piano e retta
Piano E:
¯¯¯¯¯¯¯
E: x + y + z = 5
Retta g:
¯¯¯¯¯¯¯
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Il punto di intersezione:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
S (5|0|0)
L'angolo di intersezione:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 54.73561°
Sfera e retta
La sfera:
¯¯¯¯¯¯¯¯¯
K: M (5|5|5), r = 5
La retta:
¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Punti di intersezione:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
S1 (2.81867|1.81867|1.81867)
S2 (8.51467|7.51467|7.51467)
Lunghezza della corda:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
s = 9.8657657
Due piani
I due piani:
¯¯¯¯¯¯¯¯¯¯¯
E1: 5·x - 2·y = 5
E2: 2·x - y + 5·z = 8
La retta di intersezione:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧-11 ⎫ ⎧ 10 ⎫
g : x = ⎪-30 ⎪ + r·⎪ 25 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
La distanza dall'origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1.5057283
L'angolo tra i piani:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
alfa = 65.993637°
Due sfere
Sfere: ¯¯¯¯¯ K1: M1(3|3|3), r1 = 3 K2: M2(1|1|1), r2 = 3 Cerchio di intersezione: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2), r = 2.4494897 Piano di intersezione: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ E: x + y + z = 6
Sfera e piano
Piano:
¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
La sfera:
¯¯¯¯¯¯¯¯
⎧ -> ⎧ 1 ⎫⎫2
K : ⎪ x - ⎪ 2 ⎪⎪ = 16
⎩ ⎩ 3 ⎭⎭
Cerchio di intersezione:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(1|1|1), r = 2
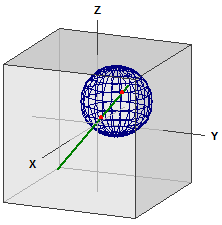
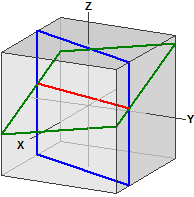
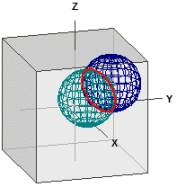
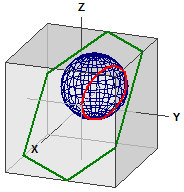
Distance sulla sfera
(Nuovo nella versione 9.0 da dicembre 2021)
Viene calcolata la distanza tra due punti su una sfera. Il programma è adatto anche per convertire i gradi decimali in gradi, minuti e secondi (dms) e viceversa.
GPS decimale ¯¯¯¯¯¯¯¯¯¯¯¯ Berlin : 52.523403, 13.4114 New York : 40.714268, -74.005974 GPS dms ¯¯¯¯¯¯¯ Berlin : 52° 31' 24.2508" N, 13° 24' 41.0400" E New York : 40° 42' 51.3648" N, 74° 0' 21.5064" W . . . Distanza ¯¯¯¯¯¯¯¯ d = r · α [rad] = 6385,112
