MatheAss 10.0 − Algebra
Numeri primi
I numeri primi tra due numeri naturali a e b sono calcolate.
Numeri primi tra 1000000000 e 1000000300: 1000000007 1000000009 1000000021 1000000033 1000000087 1000000093 1000000097 1000000103 1000000123 1000000181 1000000207 1000000223 1000000241 1000000271 1000000289 1000000297 16 Numeri primi
Tuple prime (Nuovo nella versione 9.0)
Il programma determina tutti i gemelli primi (p,p+2), i cugini primi (p,p+4), i primi sexy (p,p+6) e le triplette prime in un intervallo [a,b].
Triplette prime tra 1 e 200 (3|5|7) (5|7|11) [7|11|13] (11|13|17) [13|17|19] (17|19|23) [37|41|43] (41|43|47) [67|71|73] [97|101|103] (101|103|107) [103|107|109] (107|109|113) (191|193|197) [193|197|199] 15 tuple di triplette prime 7 del modulo (p|p+2|p+6) e 7 del modulo [p|p+4|p+6]
 Fattorizzazione in primi
Fattorizzazione in primi
Le fattorizationi in primi di numeri naturali n <1014 sono calcolato.
99999999999901 = 19001 5262880901
99999999999001 = 107 401 1327 1756309
99999999990001 = Prime
3938980639167 = 3 14 7 7
999330136292431 = 99971 2 99991
 MCD e MCM
MCD e MCM
Il massimo comune divisore, il minimo comune multiplo e il insieme di divisori di fino a 10 numeri sono calcolati.
a = 24
b = 256
Il massimo comune divisore MCD = 8
Il minimo comune multiplo MCM = 768
Insieme di divisori :
T(a) = { 1 2 3 4 6 8 12 24}
T(b) = { 1 2 4 8 16 32 64 128 256}
 Calcolo delle percentuali
(Nuovo nella versione 9.0)
Calcolo delle percentuali
(Nuovo nella versione 9.0)
Se vengono inseriti due valori indipendenti, vengono calcolati il valore base G, il valore percentuale W, la percentuale p o p%, il fattore di crescita e il valore finale E.
Dato
¯¯¯¯
Valore percentuale W = -120
Fattore di crescita q = 95% = 0,95 = 19/20
Risultati
¯¯¯¯¯¯
Valore base G = 2400
Percentuale p% = -5% = -0,05 = -1/20
Valore finale E = 2280
 Numeri decimali in frazioni
Numeri decimali in frazioni
Decimali periodiche saranno trasformati in frazioni. .
___ 1.20045 = 120/100 + 1/2220 = 533/444
 Frazioni in numeri decimali
Frazioni in numeri decimali
Le frazioni saranno trasformati in decimali periodici e anche il periodo e la lunghezza sono determinate.
___ 533/444 = 1.20045 Periodica dal 3. cifra decimale. La lunghezza del periodo è 3 cifre.
 Binomi di grado n
Binomi di grado n
La formula binomiale (a + b)2 = a2 + 2ab + b2 è sicuramente una delle formule più conosciute nella matematica scolastica.
Il programma calcola il caso più generale (a · x + b · y)n.
(2·x - 3·y)7 = +128·x7
−1344·x6 · y
+6048·x5 · y2
−15120·x4 · y3
+22680·x3 · y4
−20412·x2 · y5
+10206·x · y6
−2187·y7
 Equazioni di grado 4
Equazioni di grado 4
Il programma determina le soluzioni a valori reali di un'equazione di 4° o grado inferiore. Per equazioni di grado superiore non esiste un metodo di soluzione algebrica a parte i calcoli approssimativi (zeri nel programma Studio di funzioni arbitrarie).
x4 + 2·x3 - 3·x2 + 5·x - 5 = 0 <=> (x - 1)·(x3 + 3·x2 + 5) = 0
L = {-3,42599; 1}
 Equazioni diofanti
Equazioni diofanti
Le soluzioni intere di a·x + b·y + c = 0 con a, b, c interi sono calcolati.
Questo ad esempio permette la determinazione dei punti interi in linea retta.
7·x − 3·y − 5 = 0 ; x,y intero
L = { ( 2 + 3t | 3 + 7t ) }
 Terne pitagoriche
Terne pitagoriche
Le terne pitagoriche sono le soluzioni intere (x, y, z) dell'equazione x2 + y2 = z2, che si applica al lati in triangoli rettangoli.
Per x, y, z tra 100 e 400 otteniamo:
( 119, 120, 169 ) ( 104, 153, 185 ) ( 133, 156, 205 ) ( 105, 208, 233 ) ( 140, 171, 221 ) ( 115, 252, 277 ) ( 120, 209, 241 ) ( 161, 240, 289 ) ( 160, 231, 281 ) ( 207, 224, 305 ) ( 175, 288, 337 ) ( 135, 352, 377 ) ( 136, 273, 305 ) ( 204, 253, 325 ) ( 225, 272, 353 ) ( 189, 340, 389 ) ( 180, 299, 349 ) ( 252, 275, 373 ) ( 152, 345, 377 ) ( 228, 325, 397 )
 Calcolatrici
Calcolatrici
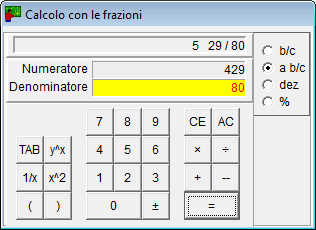
- Il calcolatore per le frazioni può eseguire le quattro operazioni aritmetiche di base e può aumentare le frazioni alla potenza.
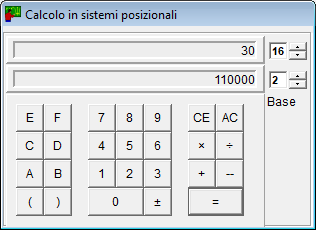
- Il calcolatore per i sistemi di valore posizionale funziona con ogni base compresa tra 2 e 16.
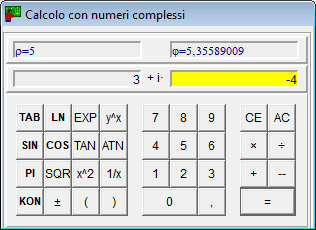
- Oltre alle normali funzioni, la calcolatrice per numeri complessi calcola anche i complessi coniugati di un numero.
Calcolo con numeri interi grandi (Nuovo nella versione 9.0 da aprile 2021)
Il calcolo si basa su numeri interi con un massimo di 10.000 cifre.
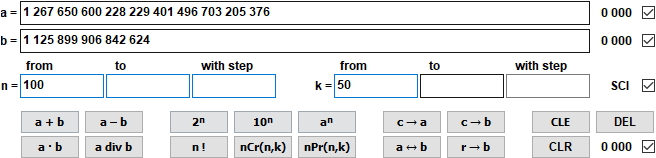
1 267 650 600 228 229 401 496 703 205 376 div 1 125 899 906 842 624 = 1 125 899 906 842 624 resto 0 = 1,13 · 10^15 resto 0 nCr(100,50) = 100 891 344 545 564 193 334 812 497 256 = 1,01 · 10^29

