MatheAss 10.0 − Stochastica
Statistica
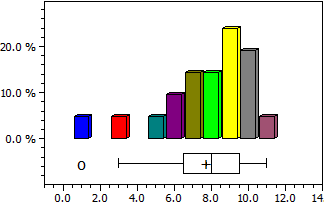
Per un elenco principale vengono determinati la media (media aritmetica), il valore centrale (mediana), la varianza e la deviazione standard. Inoltre, la distribuzione viene emessa come istogramma e come box plot.
Date
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Numero di date n = 21
Massimo max = 11
Minimo min = 1
Media x = 7,7142857
Mediana c = 8
Varianza s2 = 6,1142857
Deviazione standard s = 2,4727082
Regressione
Con questa routine, puoi eseguire un'approssimazione della curva ad una serie di punti assegnati. È possibile scegliere tra le seguenti approssimazioni e, se necessario, spostare o allungare tutti i punti nella direzione x o y.
Regressione proporzionale ( y = a·x )
Regressione lineare ( y = a·x + b )
Regressione polinomiale n-esimo ordine ( y = a0 + ... + an·xn )
Regressione geometrica ( y = a·xb )
Regressione esponenziale ( y = a·bx )
Regressione logaritmica ( y = a + b·ln(x) )
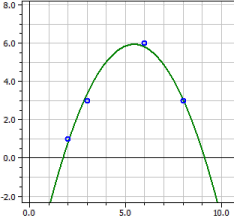
Regressione polinomiale
y = - 6,9152542
+ 4,7189266·x
- 0,43361582·x2
Coeff.of determin. = 0,98338318
Correlation coeff. = 0,99165679
Standard deviation = 0,46028731
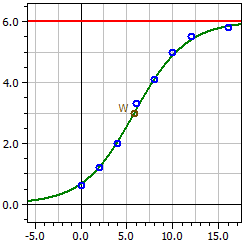
Regressione logistica (Nuovo nella versione 9.0)
Il programma determina per una serie di misurazioni una curva adatta alla funzione logistica
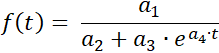
con i parametri
a1 = ƒ(0)·S , a2 = ƒ(0) , a3 = S - ƒ(0) , a4 = -k·S e il limite di saturazione S .
Dati da: "\Hopfenwachstum.csv"
Limite di saturazione: 6
Figura scura: 1
Saturation limit: 6
Dark figure: 1
4,0189
ƒ(x) = ————————————————
0,66981 + 5,3302 · e^(-0,35622·t)
Punto di flesso W(5,8226/3)
Tasso di crescita massimo ƒ'(xw) = 0,53433
8 valori
Coeff. di determinazione = 0,99383916
Coeff. di correlazioneâ€&Permil; = 0,99691482
Deviazione standardâ€&Permil; = 0,16172584
Combinatorio
Il numero di possibilità per selezionare k da n elementi viene calcolato se l'ordine è valutato o meno e se le ripetizioni sono consentite o meno.
n = 49, k = 6 Disposizione, senza ripetizione = 10 068 347 520 Disposizione, con ripetizione = 13 841 287 201 Combinazioni, senza ripetizione = 13.983.816 Combinazioni, con ripetizione = 25 827 165 Permutazione di k: k! = 720
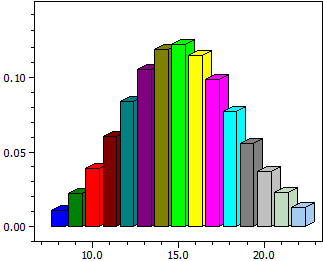
Distribuzione binomiale
Per una variabile casuale X distribuita b(K;n;p) con n e p fissa ricevete
− un istogramma delle probabilità P(X=k),
− una tabella dei loro valori dal kmin a kmax
− e la probabilità P(kmin≤X≤kmax).
n = 50 p = 0,3
k P(X=k) P(0<=X<=k)
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
8 0,01098914 0,01825335
9 0,02197829 0,04023163
10 0,03861899 0,07885062
11 0,06018544 0,13903606
12 0,08382972 0,22286578
13 0,10501745 0,32788324
14 0,11894834 0,44683157
15 0,12234686 0,56917844
16 0,11470018 0,68387862
17 0,09831444 0,78219306
18 0,07724706 0,85944012
19 0,05575728 0,91519740
20 0,03703876 0,95223616
21 0,02267679 0,97491296
22 0,01281092 0,98772387
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
P(8<=k<=22) = 0,98045967
Distribuzione ipergeometrica
Per una variabile casuale X distribuita h(K,n,m,r) con n, m e r fissa ricevete
− un istogramma delle probabilità P(X=k),
− una tabella dei loro valori dal kmin a kmax
− e la probabilità P (kmin≤X≤kmax).
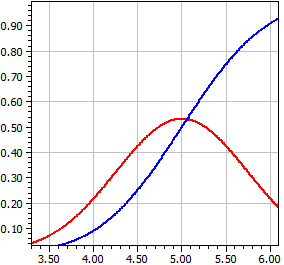
Distribuzione normale
Per una variabile casuale X distribuita N(µ, σ2) con il medio μ e la varianza σ2 ricevete la funzione di densità ƒ(x) e la funzione di distribuzione Φ(x), cioè l'integrale su ƒ(x).
μ = 5 , σ = .75
x ƒ(x) Φ(x)
¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
2 0,00017844 0,00003167
2,33333333 0,00095649 0,00018859
2,66666666 0,00420802 0,00093192
2,99999999 0,01519465 0,00383038
3,33333332 0,04503153 0,01313415
3,66666665 0,10953585 0,03772017
3,99999998 0,21868009 0,09121120
4,33333331 0,35832381 0,18703139
4,66666664 0,48189843 0,32836063
4,99999997 0,53192304 0,49999998
5,3333333 0,48189845 0,67163934
5,66666663 0,35832383 0,81296859
5,99999996 0,21868012 0,90878878
6,33333329 0,10953586 0,96227982
6,66666662 0,04503154 0,98686585
6,99999995 0,01519465 0,99616962
7,33333328 0,00420802 0,99906808
7,66666661 0,00095649 0,99981141
7,99999994 0,00017844 0,99996833
